ある不動点について計算機を回すということ
田森さんに教えてもらった数字について計算してみた。
広義の4桁の数字を考える。
ただし、0で始まる数字も含めて、4つ数字が並んだものとする。
これに対して、各桁の数字を降順(大きい順)に並べ替えた数字から
昇順(小さい順)に並べ替えた数字を引き算する操作を繰り返す。
たとえば、今年の2009から始めると、
2009
-> 9200 - 0029 = 9171
-> 9711 - 1179 = 8532
-> 8532 - 2358 = 6174
-> 7641 - 1468 = 6174
・・・・・・
となって、何度か繰り返すうちにどこかに収束したりする。
でも他の数字からスタートしても、いつも同じところに行き着く。

適当に選んだ21個の4桁の数字から出発して操作を繰り返したところ。
収束までのステップ数ごとに3通りずつ選んだので7×3=21通り。
やや分かりにくいけれど、操作のたびに一段ずつ上から下に降りていく。
曲線でつないでいるのは特に意味はなくて、重なると見にくいから。
途中で線が重なり始めて、同じようなところを進むことが分かる。
本当にどんな数字から始めても同じ点に収束するか計算する。
0000から9999まで10000個しかないので、力ずくで計算。
ただし実際は、各桁の数字の順番は関係がないので、
670通りしか数字の組み合わせはない。のだが、場合分けが
面倒なので、10000通り全部計算しよう。計算機さまさま。

どこからスタートしても7回目までには6174に収束する。
ただし、全部ゾロ目から始めたときだけすぐ0に収束する。
数字ごとに何回目で収束するかという分布を調べてみた。

だいたい一様に広がっているように見えるけれど、
ところどころはっきり「隙間」が空いていて、
この隙間はなぜ生じるのか、よくわからない。なぜ?
さっきの図だとそれぞれ何点ずつあるのか見えないので、
今度はヒストグラムにしてみた。
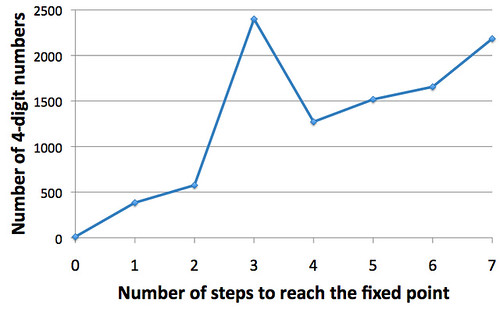
収束するまでの平均ステップ数は、4.66±1.78回(Mean±SD)。
3回のところがなければlinearに増えてるようにも見える。
たった3回の操作で収束する数が一番多いというのは不思議。
その次に多いのが、7回かかるものだけど、でも7回だけで
やっぱり6174に行き着くというのはかなり収束が早い。
たぶん、この操作が何をしているのかということを
直観的に把握できていないからそう思うのだろう。
答えを知らなければ、たとえばパイこね変換みたいに
あっち行ったりこっち行ったりふらふらし続けて
カオス的にふるまうんじゃないかと想像しがちだけど、
案外単純にどんどんアトラクターに吸い寄せられる。
F. Poyoで検索したら田森さんの"MatheMuseMent"のページを見つけた。
この数字について、p進数バージョンも合わせて詳説されてた。
F. Poyo, "7641 in N-figures and p-adic." June 6, 1996.
飯野君が昔計算して見せてくれた循環整数を思い出す。
あれもp進数で説明ができるかもしれないと言ってた。
計算としては四則演算しかしていないけれど、
今回、久しぶりにC言語をいじったのが楽しかった。
Macになってからプログラミングしたのは始めてかも。
gccでコンパイルして、gnuplotとAquaTermで表示して、
最初はばんばんエラーが出るわけだけれど、それで
どこにバグが潜んでいるのか探す作業の繰り返し。
でも、やっているうちに必ずできるというのがいい。
手を動かしているうちに少しずつでも進んでいるのが
分かるという感覚を持てるということがうれしい。
そうなっていない、どちらかと言えば苦痛に近いくらい、
いやむしろ痛みすら感じられない、無痛というのが危険。
7641-1467で検索したら、この数字には名前が付いていて、
インド人数学者に因んでKaprekar numberと言うらしい。
One of his most fascinating discoveries is
the Kaprekar constant, or 6174 (1949)[4]
....
A similar constant for 3 digits is 495[5]. However,
in base 10 a single such constant only exists for
numbers of 3 or 4 digits.
D. R. Kaprekar (en.Wiki)
田森さんも独立に発見したそうなので、すごいな。
唐突ながら、ラマヌジャンの言葉も見つけたので引用。
あるとき、ペトロス(6/12の雑記帳参照)がこのラマヌジャンに
恐る恐る訊きました。「ゴールドバッハ予想」についてはどう思う、
と。するとこんな答えが…
「直感だが、この予想は非常に大きな数については成り立たないような気がする。」
実際、大きな数になると、素数の数が減っていきます。
10億の単位になると、100個の整数の中に5個くらいになります。
しかし、400兆を超えても反例は見つかっていません。
ペトロスには衝撃的な返事だったことでしょう。ただし、
ラマヌジャンは間違うこともある、と自分に言い聞かせて
彼は研究を続けたそうです
間違うこともある、と言い聞かせながら研究を続ける
というところがなんだか素敵。
たぶん、間違うかどうかなんて気にしてなかったんだ。
ナンバーズ4に当たるかどうかよりも、その祈りを捧げ、
打ち込む姿勢に数学の女神が微笑んで欲しいと願う。
夢の中でナマギーリ女神が囁いたラマヌジャンのように。